Interpolacion:
PENDULO SIMPLE:
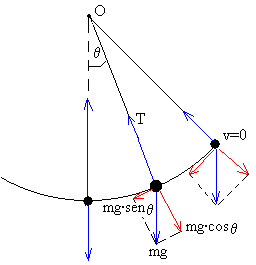
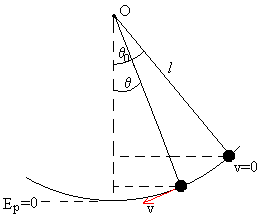
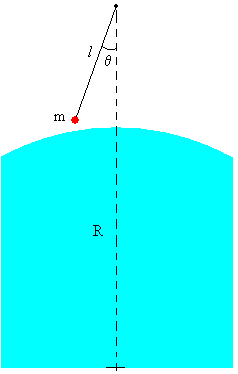
Un péndulo simple se define como una partícula de masa m suspendida del punto O por un hilo inextensible de longitud l y de masa despreciable.
Si la partícula se desplaza a una posición q0 (ángulo que hace el hilo con la vertical) y luego se suelta, el péndulo comienza a oscilar
El péndulo describe una trayectoria circular, un arco de una circunferencia de radio l. Estudiaremos su movimiento en la dirección tangencial y en la dirección normal.
Las fuerzas que actúan sobre la partícula de masa m son dos
Si la partícula se desplaza a una posición q0 (ángulo que hace el hilo con la vertical) y luego se suelta, el péndulo comienza a oscilar
El péndulo describe una trayectoria circular, un arco de una circunferencia de radio l. Estudiaremos su movimiento en la dirección tangencial y en la dirección normal.
Las fuerzas que actúan sobre la partícula de masa m son dos
- el peso mg
- La tensión T del hilo
Descomponemos el peso en la acción simultánea de dos componentes, mg·senq en la dirección tangencial y mg·cosq en la dirección radial.
v2=2gl(cosθ-cosθ0)
La tensión de la cuerda es
T=mg(3cosθ-2cosθ0)
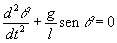 El movimiento de un péndulo simple es como un movimiento armónico simple en donde la ecuación para el desplazamiento angular es
El movimiento de un péndulo simple es como un movimiento armónico simple en donde la ecuación para el desplazamiento angular es
- Ecuación del movimiento en la dirección radial
La aceleración de la partícula es an=v2/l dirigida radialmente hacia el centro de su trayectoria circular.
La segunda ley de Newton se escribe
man=T-mg·cosq
Conocido el valor de la velocidad v en la posición angular q podemos determinar la tensión T del hilo.
La tensión T del hilo es máxima, cuando el péndulo pasa por la posición de equilibrio, T=mg+mv2/l
Es mínima, en los extremos de su trayectoria cuando la velocidad es cero, T=mgcosq0
- Principio de conservación de la energía
En la posición θ=θ0 el péndulo solamente tiene energía potencial, que se transforma en energía cinética cuando el péndulo pasa por la posición de equilibrio
Comparemos dos posiciones del péndulo:
En la posición extrema θ=θ0, la energía es solamente potencial.
E=mg(l-l·cosθ0)
En la posición θ, la energía del péndulo es parte cinética y la otra parte potencial
|
La energía se conserva
v2=2gl(cosθ-cosθ0)
La tensión de la cuerda es
T=mg(3cosθ-2cosθ0)
La tensión de la cuerda no es constante, sino que varía con la posición angular θ. Su valor máximo se alcanza cuando θ=0, el péndulo pasa por la posición de equilibrio (la velocidad es máxima). Su valor mínimo, cuando θ=θ0 (la velocidad es nula).
- Ecuación del movimiento en la dirección tangencial
La aceleración de la partícula es at=dv/dt.
La segunda ley de Newton se escribe
mat=-mg·senq
La relación entre la aceleración tangencial at y la aceleración angular a es at=a ·l. La ecuación del movimiento se escribe en forma de ecuación diferencial
Movimiento del pendulo:
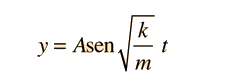
| 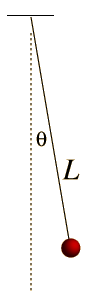 |
| La frecuencia del péndulo en Hz está dada por | 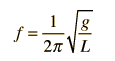 |
| y el periodo del movimiento es entonces | 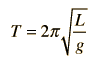 } |
Periodo del pendulo:
Una masa puntual colgando de una cuerda sin masa, es un ejemplo idealizado de un péndulo simple. Cuando se desplaza desde su punto de equilibrio, la fuerza de restauración que lo trae de nuevo al centro, está dada por:
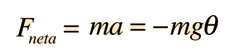  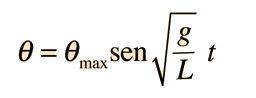
|

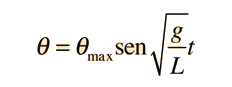
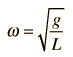
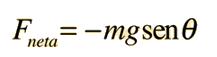
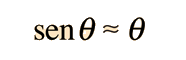
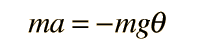
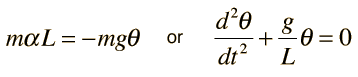



No hay comentarios:
Publicar un comentario